Thursday, September 26, 2013
Tuesday, September 17, 2013
Monday, September 16, 2013
Monday, September 2, 2013
Thursday, August 29, 2013
Wednesday, August 28, 2013
A completely pan-and-zoomable picture of the Milky Way galaxy
Go Bigger...
Bigger Still....
Even bigger....
Behold! This is the star-forming region G305, an enormous cloud of gas about 12,000 light years away which is busily birthing stars. About 10,000 stars can be seen in this photo.
And here's another zoom-able picture by Stéphane Guisard at the ESO's Paranal Observatory in Chile
The above image shows an area of the sky that is about twice of what you can cover up with your outstretched hand. It is a mosaic shot over the course of 29 nights for a total of 200 hours of exposure over 1200 separate photos.
There are tens of millions of stars in this picture at least. And this is less than one-thousandth of all the stars you can see in the night sky!
Tuesday, August 27, 2013
Monday, August 26, 2013
Sunday, August 18, 2013
Daylight Hours Explorer
Curious about how many daylight hours you are going to enjoy today? Simply punch in your latitude and the day and SHAZAM!
Daylight Hours Explorer can displays the yearly average. Dallas (32.82-degrees North) receives an average of 11 hours 6 minutes of daylight over the course of a year. Today, September 18th, Dallas will receive 13 hours and and 6 minutes because the Earth's axis is tilted ~24.4-degrees and currently pointing toward the Sun, making the days slightly longer right now. If you were standing directly above Earth's northern axis (90-degrees North), you currently be getting full daylight around-the-clock, and it would stay that way until September 23rd. Then, suddenly you'd be getting no daylight during the day -- 6 months of night!
You can check on your own latitude's stats by finding your location in Google Maps and reading the the URL:
For instance:
https://www.google.co.in/maps/preview#!data=!1m4!1m3!1d788!2d88.4328534!3d22.6145349Longitude: 88.4328534
Latitude: 22.6145349
Have fun!
Tuesday, August 13, 2013
Aristarchus' method of estimating the size and distance of the Moon
Aristarchus, all the way back in ~300 BCE, measured the angular separation of the Sun and the Moon when seen during its first or third quarter phases.
He measured the angular distance between the Moon and the Sun and determined it was "one-thirteen of a quadrant" (~3 degrees) less than vertical 90 degrees, or ~87 degrees. From this he determined that the length to the Sun (S) was about ~19-times longer than the length to the Moon (L).
*The true value of this angle is closer to 89.85(0) degrees, and so the Sun's distance is actually about 389-times the Moon's distance to the Earth. As you can see, only a small 2.85 degree (3.17%) error in the angle estimate resulted in a ~20-fold error in the distance. Yikes! This probably is a result of the fact that 1) it's hard to know exactly when the Moon is half-full and thus creating the exactly 90 degree angle, and 2) he had to estimate the relative depths to the center of the Earth, the Moon and the Sun and, as we know, Aristarchus could've have possibly imagined how huge the Sun was prior to determining its distance.
Never-the-less, Aristarchus did show that the Sun was very, very far away (or much farther away than the Moon).
Aristarchus knew that occasionally, the Moon would pass entirely through the shadow cast by the Earth: a total lunar eclipse. He saw this as an excellent opportunity to estimate the radius of the Moon.
First he measured the time it took from the moment when the edge of the Moon first entered the full shadow (the umbra) and the moment when the Moon was first totally eclipsed. At the same time, Aristarchus also measured the total duration of eclipse. He found that both times were the same, so the Moon must be only half as wide as Earth's shadow. In other words, he concluded that the diameter of the Moon was ~0.5 times diameter of the Earth.
Drawing what he felt was the correct conformation of a total lunar eclipse, he reasoned that:
Since (s / ℓ) = 19.1, and (d / ℓ) = 2:
(1 + (ℓ / s)) / (1 + (d / ℓ)) = (ℓ / t)
(1 + (1 / 19.1)) / (1 + 2) = (ℓ / t) = 1 / 2.85
In other words, the Earth's diameter was 2.85 times the diameter of the Moon. The actual ratio is about 3.7.
Again, we see that Aristarchus' mistake measurement error for the correct angle on the quarter-moons angle brings the 19.1 /1 (S / L) ratio (versus the actual 389 /1 ratio) and applies the same errant ratio to (s / ℓ), which would also be ~389/1. Small errors, especially ones applied trigonometry, lead to big errors.
He also determined that:
(1 + (s / ℓ) / (1 + (d / ℓ)) = (s / t)
(1 + 19.1) / (1 + 2) = (s / t) = 6.70
In other words, Aristarchus estimated that the Sun's radius was 6.7 times larger than the Earth's radius. The real ratio is 109.
[List of Aristarchus' Propositions]
[Aristarchus' On the Sizes and Distances]
A solid effort, none-the-less. Later Hipparchus did a bit better. Giovanni Cassini later complete the job by using the observed parallax of Mars to determine the distance of all the planets in the Solar System.
Below are the actual distances:
*NOT TO SCALE
He measured the angular distance between the Moon and the Sun and determined it was "one-thirteen of a quadrant" (~3 degrees) less than vertical 90 degrees, or ~87 degrees. From this he determined that the length to the Sun (S) was about ~19-times longer than the length to the Moon (L).
*The true value of this angle is closer to 89.85(0) degrees, and so the Sun's distance is actually about 389-times the Moon's distance to the Earth. As you can see, only a small 2.85 degree (3.17%) error in the angle estimate resulted in a ~20-fold error in the distance. Yikes! This probably is a result of the fact that 1) it's hard to know exactly when the Moon is half-full and thus creating the exactly 90 degree angle, and 2) he had to estimate the relative depths to the center of the Earth, the Moon and the Sun and, as we know, Aristarchus could've have possibly imagined how huge the Sun was prior to determining its distance.
Never-the-less, Aristarchus did show that the Sun was very, very far away (or much farther away than the Moon).
Aristarchus knew that occasionally, the Moon would pass entirely through the shadow cast by the Earth: a total lunar eclipse. He saw this as an excellent opportunity to estimate the radius of the Moon.
First he measured the time it took from the moment when the edge of the Moon first entered the full shadow (the umbra) and the moment when the Moon was first totally eclipsed. At the same time, Aristarchus also measured the total duration of eclipse. He found that both times were the same, so the Moon must be only half as wide as Earth's shadow. In other words, he concluded that the diameter of the Moon was ~0.5 times diameter of the Earth.
Aristarchus also knew that during a total solar eclipse, the Moon's body nearly perfectly covered the Sun. He cleverly reasoned that since he had earlier shown that the Sun was 19.1-times farther way from Earth than the Moon, that since they are nearly the same size in the sky, the Sun's radius must be ~19.1-times larger than than the Moon's to keep their apparent sizes seen from Earth correct.
Since (s / ℓ) = 19.1, and (d / ℓ) = 2:
(1 + (ℓ / s)) / (1 + (d / ℓ)) = (ℓ / t)
(1 + (1 / 19.1)) / (1 + 2) = (ℓ / t) = 1 / 2.85
In other words, the Earth's diameter was 2.85 times the diameter of the Moon. The actual ratio is about 3.7.
Again, we see that Aristarchus' mistake measurement error for the correct angle on the quarter-moons angle brings the 19.1 /1 (S / L) ratio (versus the actual 389 /1 ratio) and applies the same errant ratio to (s / ℓ), which would also be ~389/1. Small errors, especially ones applied trigonometry, lead to big errors.
He also determined that:
(1 + (s / ℓ) / (1 + (d / ℓ)) = (s / t)
(1 + 19.1) / (1 + 2) = (s / t) = 6.70
In other words, Aristarchus estimated that the Sun's radius was 6.7 times larger than the Earth's radius. The real ratio is 109.
[List of Aristarchus' Propositions]
[Aristarchus' On the Sizes and Distances]
A solid effort, none-the-less. Later Hipparchus did a bit better. Giovanni Cassini later complete the job by using the observed parallax of Mars to determine the distance of all the planets in the Solar System.
Below are the actual distances:
The Moon is 384,400 km (238,900 miles), on average, from the Earth. This varies because the Moon is in a elliptic orbit around the Earth. [image]
![[image]](http://en.wikipedia.org/wiki/File:Lunar_perigee_apogee.png){kind=link}
The Moon-Earth distance is actually increasing by ~38 mm per year because of a phenomena known as tidal-locking.
The Earth is about 149,597,870.700 km (92,955,807.273 miles) from the Sun
Estimating the Astronomical Unit
In order to measure the distance between the something and something very far away, it is helpful to have a third referencing object (an imaginary point origin, a stick, a tree, a planet a star, etc.)
The best way we can estimate the distance between the Sun and the Earth (the astronomical unit) is by measuring the angular difference between Venus' location and the Sun (e). There are two points in Venus' orbit around the Sun where an imaginary line joining Earth and Venus will be 90 degrees from an imaginary line connecting Venus to the Sun. We observe this as being the greatest visible distance points of Venus compared to the Sun during the year (at dawn or at sunset).
[Simulation]
These points are called "the points of greatest elongation."
*NOT TO SCALE*
Using a bit of trig(onometry), if we can accurately determine the distance between Earth and Venus, which is a*cos(e) , then we can divide that distance by cos(e) and solve for a, the Astronomical Unit.
The best way we can estimate the distance between the Sun and the Earth (the astronomical unit) is by measuring the angular difference between Venus' location and the Sun (e). There are two points in Venus' orbit around the Sun where an imaginary line joining Earth and Venus will be 90 degrees from an imaginary line connecting Venus to the Sun. We observe this as being the greatest visible distance points of Venus compared to the Sun during the year (at dawn or at sunset).
[Simulation]
These points are called "the points of greatest elongation."
Using a bit of trig(onometry), if we can accurately determine the distance between Earth and Venus, which is a*cos(e) , then we can divide that distance by cos(e) and solve for a, the Astronomical Unit.
We can determine the distance between Earth and Venus: by radar. Knowing this, we determined the astronomical unit with great accuracy in 1960s.
THE IMPORTANCE OF TRANSIT EVENTS
You can also accurately estimate the distance to the Sun by observing a parallax created with Venus (or Mercury) passes or "transits" across the face of our Sun, viewed from two different locations on Earth.
If you know the absolute distance (not surface distance, remember, Earth is a oblate sphere) between viewpoints A and B, you can determine the distance in kilometers from Earth to Venus as:
0.5*(Distances A-B) / tan(0.5*(Angular difference between positions of Venus from seen from points A and B in the sky))
Using Kepler's Third Law of Planetary Motion, we can estimate that the distance Earth and Venus is only 28% the distance of the Earth to the Sun, so:
Distance Earth to Venus / 0.28 = Distance of Earth to the Sun
Monday, August 12, 2013
A year of San Francisco sky
Artist Ken Murphy created this interesting video by installing a camera on the roof of the Exploratorium Museum in San Francisco. It took a picture every ten seconds for the full year, starting in July 2009. The upper left corner shows the sky on July 28, 2009, and then each successive day is in the next rectangle over all the way to July 2010.
Notice that in the summer day frames (top and bottom rows), the days are longer because the Sun rises earlier and sets later. The winter days are in the middle rows, and the Sun rises later and sets earlier.
The difference in the Sun's rising and setting times throughout the year is due to the fact that the Earth's axis of rotation is tilted approximately -23.4 degrees from the 90 degrees from the imaginary plane of its orbit around the Sun (its ecliptic). This causes the northern hemisphere to be tilted slightly towards the Sun at the end of March-September and away from the Sun at the end of September-March.
Video from NASA's METEOSAT-9 meteorological satellite showing the shifting of Earth's day-night line as the Earth orbits the Sun.
Around 6 a.m. local time each day, the Sun, Earth, and any geosynchronous satellite form a right angle to the day-night line (the edge between the shadows of nightfall and the sunlight of dusk and dawn).
[NASA Source]
Notice that in the summer day frames (top and bottom rows), the days are longer because the Sun rises earlier and sets later. The winter days are in the middle rows, and the Sun rises later and sets earlier.
The difference in the Sun's rising and setting times throughout the year is due to the fact that the Earth's axis of rotation is tilted approximately -23.4 degrees from the 90 degrees from the imaginary plane of its orbit around the Sun (its ecliptic). This causes the northern hemisphere to be tilted slightly towards the Sun at the end of March-September and away from the Sun at the end of September-March.
Because of this tilt, each spot in the northern hemisphere either receives slightly more time on the "day-side" of the Earth, or less time. As the Earth continues around its in its yearly orbit, this pattern flips so that they southern hemisphere no receives slightly more time on the "day-side". The increase of Sun-time and the more direct angle the Sun's light reaches the Earth's surface in the northern hemisphere are the reason we have seasons here on Earth (not really the Earth's proximity to the Sun).
Video from NASA's METEOSAT-9 meteorological satellite showing the shifting of Earth's day-night line as the Earth orbits the Sun.
Around 6 a.m. local time each day, the Sun, Earth, and any geosynchronous satellite form a right angle to the day-night line (the edge between the shadows of nightfall and the sunlight of dusk and dawn).
[NASA Source]
Socrative - FREE Student Clicker on your Andriod/iPhone
 |
| App for iPhone |
 |
| App for Andriod |
The Socrative app turns your phone into a smart clicker! See all your classmates’ ideas in real-time so that you can interact with and evaluate the responses. This provides your instructor (me) valuable feedback on their lessons and can help demonstrate how well you understand the material. Have Fun!
Friday, August 9, 2013
The Reason for Earth's Seasons
The Earth's orbit is an ellipse, and as such there are times where Earth is closer to the Sun or farther; however Earth's distance from the Sun is NOT the primary reason Earth has distinct seasons.
Our first clue is that the Earth reaches its closes point to the Sun ("perihelion") in January, and it reaches its farthest point from the Sun ("aphelion") six months later. Together these are called Earth's "solstice" positions If the Sun's distance was the main thing that governed our weather, we'd have our summers in January, and winter in July. This is true for the southern hemisphere but not the northern hemisphere; clearly something else is be going on.
[Earth's Solstice Dates thru 2020]
We can actually calculate the average temperature shift caused by the change in Earth's distance! First we must assume the energy that the Earth receives from the Sun on its "Sun-side" is the same as the energy radiated away by the Earth on its "night-side".
If this were not true, even slightly so, the Earth would rapidly heat up, boil away its oceans and it's crust would be melt.
*Looks out the windows*
Nope we're okay to make that assumption.
The following calculations can be derived from the Stefan-Boltzman Law, which describes the power of the energy radiating spherically (in all directions) away from an object:
The Earth passes through the Sun's energy at radius (a0) the amount of energy it experiences through each square-meter of its trip is described by:
The Earth has a radius of rE, and a cross-section area of pi * rE2, so the amount of solar power absorbed by the Earth is:
From here, you can cross-out common factors and solve for the temperature of experienced by the Earth:
So you see, since the radius and the temperature of the Sun is fairly constant, we can determine that the energy experienced by the Earth is inversely proportional to the square of its distance. At perihelion (nearest point) the Earth/Sun distance is about 147,000,000 km, while at aphelion (farthest point) its distances is about 152,000,000 km. The difference in temperature between these two points is
The Earth's varying distance from the Sun throughout the year causes only a 1% percent difference in the raw heat energy it receives! Over the course of a year, this difference alone amounts to only a ~5 C (9 F) discrepancy between summer and winter temperatures, which is quite a bit less than the temperature change most of us see.
The largest contributor to the temperature change between seasons is the -23.4 degree tilt (or "inclination") of the Earth's rotational axis with respect to its orbital plane (its "ecliptic"). Here's the classic explanation of why:
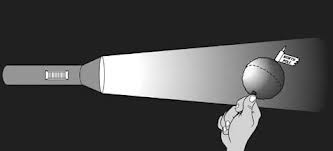
Imagine taking a flashlight and a piece of paper and shining the light straight onto the paper, so that you see a circle illuminated. From the same height slowly tilt the flashlight downwards (or the paper upwards), so that the circle elongates into an ellipse. Notice that the light now spreads out over a much larger area. Now the amount of the amount of light being put out by the flashlight is the same, but the density of the light (photons/meter2) substantially drops!
Since the Earth's rotational axis is tilted, so that the Sun appears higher in the sky when you are in the hemisphere of the Earth where the axis is pointing towards the Sun, and lower in the sky in the hemisphere whose axis is pointing away from the Sun.
When the Sun is higher overhead in summer-time, the light is falling from a higher angle to the ground in that hemisphere, and so more of the Sun's light (and heat) reaches the ground per square meter. When the Sun is lower in the winter-time, the Sun's incoming light (and heat) hits the Earth at a lower angle so its heat energy is spread out over more ground, so there is less heat per square meter being absorbed! This is the reason solar panels are placed so that they are south-facing in the northern hemisphere and north-facing in the southern hemisphere! And they are tilted up 45 degrees from the ground so that there is the least amount of energy variance over the course of the year!
[Earth's Seasons Simulator]
And there is more!. In the summer, the Sun is higher, the days are therefore slightly longer (more time on the "Sunny" side each day), giving the Sun more time to shine and heat each square meter of the Earth in that hemisphere, further increasing the temperature. In the winter, the Sun is lower, so days are slightly shorter (less time on the "Sunny" side each day), giving the Sun less time to heat the Earth, so it doesn't get as hot.
[Calculate Day-Night Times for Any Day of the Year]
Now the ~1% temperature difference between Earth's aphelion and perihelion is minor but certainly not zero! It does have a slight effect. Consequently, because the southern hemisphere's axis is tilted toward the Sun during the same time it is every-so-slightly closer to the Sun, it enjoys slightly hotter summers and slightly colder winters compared to the northern hemisphere -- but only by a few degrees, on average.
BONUS FACT:
If you actually plug in values for the equation above you might find a surprising result. Use a0 = 149.598 x 109 meters, TS = 5780 K, rs= 696 x 106 meters.
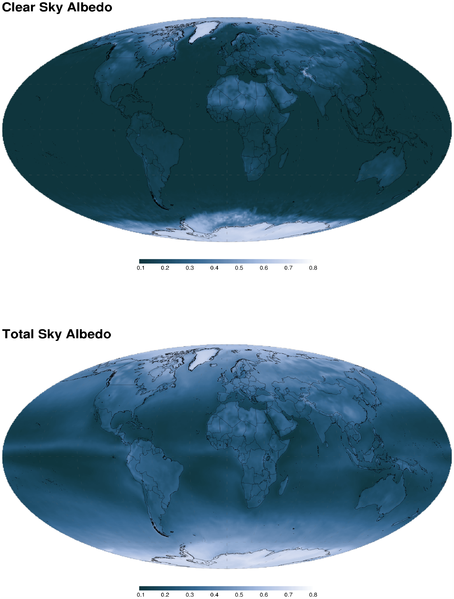
The Earth's surface actually contains a lot of reflective materials (water vapor, clouds, ocean water, ice caps, etc.) so that assuming the Earth absorbed all the Sun's energy was a bit overly optimistic. About 39% of the Sun's radiation that hits our planet immediately gets scattered back into space without any effect on its temperature.
"Albedo" is what astronomers call this percentage reflectivity. Consequently, we must multiply the value we obtained by 0.611/4. What you'll find is that your value (converted from Kelvin to Celsius) is quite a bit below 0 C! You know what happens at 0 C!?! Water freezes! A Snowball Earth!
You know why we don't have a Snowball Earth? Greenhouse gases in our atmosphere (namely water vapor, carbon dioxide and methane). This collection of molecules help absorb some of the sunlight that is being reflected by the Earth into space, and re-emit it back towards the ground.
The "greenhouse effect" helps effectively lower Earth's albedo by artificially increasing the total amount of energy that is heating the planet's surface by an extra ~33 C. This brings the temperature back well above water's freezing point, giving us a "blue" ocean planet, not a "white" glacial planet.
So, it's true; having some greenhouse gases in our atmosphere is absolutely essential for life to exist on our planet; however the amount we are now collectively pumping out is excessive. The consequence of having too many greenhouse gas molecules floating around is that more of the Sun's heat will be absorb and re-distributed in our atmosphere - causing a hotter planet. We call this increasing temperature trend global warming.
NASA Report on Earth's Temperature Anomaly Over the Last Decade (2000-2009):
[Source]
We're not quite there yet but an overwhelming amount of climate scientists fear that we are rapidly (and exponentially) approaching a break-point where Earth could succumb to a "runaway greenhouse effect."
[Source: NASA take on Climate Change]
In such a state the increasing temperatures will cause more of Earth's water molecules to evaporate; and since water vapor is a powerful greenhouse gas, its increase in the atmosphere would temperature to rise even more, causing more water to evaporate, causing more temperature rise, etc.
Do you want see what "runaway greenhouse" looks like? Merely look at Venus. Even though Venus is closer to the Sun, its thick, dense clouds cause its albedo (effective reflectivity) to be so high that actually we'd expect that planet to be fairly close to Earth's temperature. It's not. The huge amounts of greenhouse gases in Venus' atmosphere cause its surface temperature to be often in excess of 500 C (900 F)! Anything we land on Venus, quickly melts.
In other words, please support non-combustion, non-carbon producing ("green") sources of energy!
Our first clue is that the Earth reaches its closes point to the Sun ("perihelion") in January, and it reaches its farthest point from the Sun ("aphelion") six months later. Together these are called Earth's "solstice" positions If the Sun's distance was the main thing that governed our weather, we'd have our summers in January, and winter in July. This is true for the southern hemisphere but not the northern hemisphere; clearly something else is be going on.
[Earth's Solstice Dates thru 2020]
We can actually calculate the average temperature shift caused by the change in Earth's distance! First we must assume the energy that the Earth receives from the Sun on its "Sun-side" is the same as the energy radiated away by the Earth on its "night-side".
If this were not true, even slightly so, the Earth would rapidly heat up, boil away its oceans and it's crust would be melt.
*Looks out the windows*
Nope we're okay to make that assumption.
The following calculations can be derived from the Stefan-Boltzman Law, which describes the power of the energy radiating spherically (in all directions) away from an object:
The Earth passes through the Sun's energy at radius (a0) the amount of energy it experiences through each square-meter of its trip is described by:
The Earth has a radius of rE, and a cross-section area of pi * rE2, so the amount of solar power absorbed by the Earth is:
From here, you can cross-out common factors and solve for the temperature of experienced by the Earth:
So you see, since the radius and the temperature of the Sun is fairly constant, we can determine that the energy experienced by the Earth is inversely proportional to the square of its distance. At perihelion (nearest point) the Earth/Sun distance is about 147,000,000 km, while at aphelion (farthest point) its distances is about 152,000,000 km. The difference in temperature between these two points is
√(152,000,000/147,000,000) = 1.017% difference in TE
The Earth's varying distance from the Sun throughout the year causes only a 1% percent difference in the raw heat energy it receives! Over the course of a year, this difference alone amounts to only a ~5 C (9 F) discrepancy between summer and winter temperatures, which is quite a bit less than the temperature change most of us see.
The largest contributor to the temperature change between seasons is the -23.4 degree tilt (or "inclination") of the Earth's rotational axis with respect to its orbital plane (its "ecliptic"). Here's the classic explanation of why:
Imagine taking a flashlight and a piece of paper and shining the light straight onto the paper, so that you see a circle illuminated. From the same height slowly tilt the flashlight downwards (or the paper upwards), so that the circle elongates into an ellipse. Notice that the light now spreads out over a much larger area. Now the amount of the amount of light being put out by the flashlight is the same, but the density of the light (photons/meter2) substantially drops!
Since the Earth's rotational axis is tilted, so that the Sun appears higher in the sky when you are in the hemisphere of the Earth where the axis is pointing towards the Sun, and lower in the sky in the hemisphere whose axis is pointing away from the Sun.
[Earth's Seasons Simulator]
And there is more!. In the summer, the Sun is higher, the days are therefore slightly longer (more time on the "Sunny" side each day), giving the Sun more time to shine and heat each square meter of the Earth in that hemisphere, further increasing the temperature. In the winter, the Sun is lower, so days are slightly shorter (less time on the "Sunny" side each day), giving the Sun less time to heat the Earth, so it doesn't get as hot.
[Calculate Day-Night Times for Any Day of the Year]
Now the ~1% temperature difference between Earth's aphelion and perihelion is minor but certainly not zero! It does have a slight effect. Consequently, because the southern hemisphere's axis is tilted toward the Sun during the same time it is every-so-slightly closer to the Sun, it enjoys slightly hotter summers and slightly colder winters compared to the northern hemisphere -- but only by a few degrees, on average.
BONUS FACT:
If you actually plug in values for the equation above you might find a surprising result. Use a0 = 149.598 x 109 meters, TS = 5780 K, rs= 696 x 106 meters.
The Earth's surface actually contains a lot of reflective materials (water vapor, clouds, ocean water, ice caps, etc.) so that assuming the Earth absorbed all the Sun's energy was a bit overly optimistic. About 39% of the Sun's radiation that hits our planet immediately gets scattered back into space without any effect on its temperature.
"Albedo" is what astronomers call this percentage reflectivity. Consequently, we must multiply the value we obtained by 0.611/4. What you'll find is that your value (converted from Kelvin to Celsius) is quite a bit below 0 C! You know what happens at 0 C!?! Water freezes! A Snowball Earth!
The "greenhouse effect" helps effectively lower Earth's albedo by artificially increasing the total amount of energy that is heating the planet's surface by an extra ~33 C. This brings the temperature back well above water's freezing point, giving us a "blue" ocean planet, not a "white" glacial planet.
So, it's true; having some greenhouse gases in our atmosphere is absolutely essential for life to exist on our planet; however the amount we are now collectively pumping out is excessive. The consequence of having too many greenhouse gas molecules floating around is that more of the Sun's heat will be absorb and re-distributed in our atmosphere - causing a hotter planet. We call this increasing temperature trend global warming.
NASA Report on Earth's Temperature Anomaly Over the Last Decade (2000-2009):
[Source: NASA take on Climate Change]
In such a state the increasing temperatures will cause more of Earth's water molecules to evaporate; and since water vapor is a powerful greenhouse gas, its increase in the atmosphere would temperature to rise even more, causing more water to evaporate, causing more temperature rise, etc.
Do you want see what "runaway greenhouse" looks like? Merely look at Venus. Even though Venus is closer to the Sun, its thick, dense clouds cause its albedo (effective reflectivity) to be so high that actually we'd expect that planet to be fairly close to Earth's temperature. It's not. The huge amounts of greenhouse gases in Venus' atmosphere cause its surface temperature to be often in excess of 500 C (900 F)! Anything we land on Venus, quickly melts.
Subscribe to:
Posts (Atom)